네트워크: Network layer 정리3(routing algorithm, link state, distance vector)

네트워크: Network Layer 정리2(IPv4, DHCP, NAT, SDN...)

저번 포스팅에 이어 Network layer control plane에서 routing 프로토콜에 대해서 알아본다.

 

이번 포스팅은 효율적인 라우팅 알고리즘을 만들기 위해 어떤 알고리즘을 사용하는지가 주내용이다.

 

우선 라우팅 프로토콜에 대해서 알아보기 전, control plane에 대해서 한 번 더 되짚어 보고 간다.

 

 

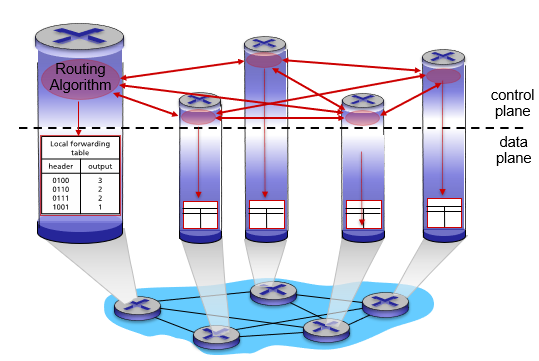
1. Per-router control plane 방식에서의 control plane의 역할

 

현재 사용되는 방식으로 router들끼리 상호작용해서 forwarding table을 만든다. 

 

 

 

 

 

2. SDN(Software Defined Networking)에서 control plane의 역할

 

control plane의 Remote Controller와 router의 control agent는 상호작용함으로써

적합한 forwarding table을 작성하고 data plane으로 내려준다. 

 

 

 

 

 

<Routing protocols>

 

routing protocol의 목표는 호스트로부터 다른 호스트까지 최적의 경로를 정하는 것이다. 

 

최적의 경로란 최소의 비용(congestion, bandwidth, distance등)을 고려하여

가장 빠르게 목적지까지 도달하는 것이며

최적의 경로를 정하기 위해 link state와 distance vector 방식이 사용된다. 

 

다음 예시를 통해 Link state와 distance vector 방식을 사용하여

어떻게 forwarding table의 path가 만들어지는지 알아본다

 

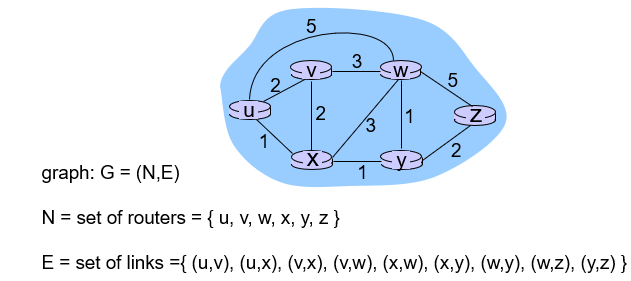
(Node는 라우터, Edge는 링크를 나타내며 총 cost가 가장 적은 경로를 찾는다)

 

 

 

1. Link state

 

모든 라우터들이 다른 링크 cost에 대한 정보를 모두 알고 있는 경우다.

 

global한 정보를 알고 알고리즘을 짜기 때문에 lilnk state 알고리즘이라고 한다. 

 

모든 노드에 대한 net topology, link cost를 다 알고 있기 때문에 다익스트라 알고리즘을 사용한다.

(여행으로 따지면 지도를 가지고 있는 셈) 

 

여기서 다익스트라 알고리즘이란 한 노드에서 주위의 모든 노드까지 가는데 최단경로를 구하는 알고리즘이다. 

 

 

 

다음은 다익스트라 알고리즘의 수도코드 

다익스트라 알고리즘 코드

 

위의 코드는 u에서 모든 경로에 대한 최단경로를 구하는 과정이다. 

 

Initializatoin에서 u에서 부터 u를 제외한 모든 노드까지의 거리를 초기값으로 정한다.

(u와 connected하지 않은 노드는 무한대로 생각한다)

 

Loop에서 N'에 속하지 않은 노드중 가장 작은 값을 기준으로 Distance를 업데이트한다.

(기존의 값과 업데이트한 값 중에 더 작은 값으로 업데이트한다)

 

업데이트가 끝나면 N'에 기준 노드를 추가하고 N'에 모든 노드가 들어갈때까지 반복한다.

 

다익스트라알고리즘

이제 이 테이블을 통해 u에서 모든 노드까지의 최단거리와 경로를 구할 수 있다.

 

예를 들어, u에서 z까지의 최단거리는 4이고, 최단 경로는 u -> x -> y ->z 이다. 

u에서 w까지의 최단거리는 3이고, 최단 경로는 u -> x -> y ->w 이다. 

u에서 v까지의 최단거리는 2이고, 최단 경로는 u -> v 이다. 

u에서 y까지의 최단거리는 2이고, 최단 경로는 u -> x -> y 이다. 

u에서 x까지의 최단거리는 1이고, 최단 경로는 u -> x 이다. 

 

즉 다음 경로가 최단 경로이다. 

 

 

 

 

2. Distance vector

 

Distance vector 알고리즘은 Link state와는 반대로 전체적인 토폴로지를 모른다.  

 

분산된 구조로써 physically connected한 neighbor들에 대한 정보만 안다. 

 

부분적인 정보밖에 모르기 때문에 반복적인 연산을 통해 neighbor이외의 정보를 알게되며

전체적인 정보는 Bellman-Ford equation 알고리즘을 이용하여 구한다.

 

Bellan-Ford equation은 dynamic programming 방식을 이용하며 

x부터 y까지의 거리 dx(y)는 다음과 같이 정의한다. 

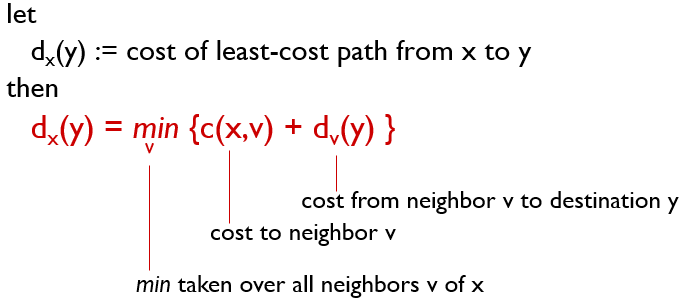
다음 예시를 통해  dx(y)가 무엇인지 확인 해보자 

u에서 z까지의 최소비용을 구하고 싶을 때 u와 연결되어 있는 노드 v, x ,w를 기준으로 비교한다. 

 

u 에서 v까지의 cost + v 에서 z까지의 최소비용 d

u 에서 x까지의 cost + x 에서 z까지의 최소비용 d

u 에서 w까지의 cost + w 에서 z까지의 최소비용 d

 

중에서 최소 값을 du(z)이라고 한다. 

 

위 과정을 다음과 같이 반복하여 값을 업데이트 한다. 

 

각 노드들은 변화가 올때까지 기다리고 변화가 생기면 estimates를 계산하여

이 값이 최적이라면 distance vector를 update하고 이를 neigbor들에게 알린다. 

 

 

 

 

※전공 공부용으로 작성했습니다.

출처: computer networking a top down approach