알고리즘: 큰 수의 곱셈 알고리즘(feat. c++ pseudocode )

빅데이터 시대에서는 엄청나게 큰 숫자를 다루는 일이 존재한다.

 

하지만 자료형들은 수를 담을 수 있는 한계가 존재하고

 

배열로 표현함으로써 더 큰 정수를 표현할 수 있다.

 

 

예를 들어, S[5]S[4]S[3]S[2]S[1] = 92420로 표현할 수 있다.

 

이런 방식으로 표현한다면 표현하지 못할 수는 없다.

 

하지만 큰 수만 표현할 수 있으면 뭐하냐 

 

효율적으로 연산이 가능해야 한다. 큰 수의 덧셈뺄셈은 많은 시간복잡도를

잡아먹지는 않지만, 곱셈의 경우에는  

 

단순한 방법으로 quadratic-time algorithm(두개의 반복문)을 이용하여

곱셈으로 자릿수를 표현하면 시간복잡도는 다음과 같다. 

 

 

 

하지만 이보다 더 좋은 큰자리수 곱셈알고리즘이 존재한다.

 

분할정복으로 이 보다 더 좋은 차수의 큰 정수 곱셈을  만들어보자

 

n-digit의 정수를 2개의 n/2-digit 정수로 분할한다.

 

 

 

정수 u, v를 각각 분할하여 나눴을때 uv값은 다음과 같다.

 

 

 

여기서 xw, xz, wy, yz을 구해서 연산을 해보면 

 

이고, 도사정리를 이용하면 

 

 

 

하지만 이는 같은 시간복잡도를 갖는 걸로 보아 의미가 없어 보일 수는 없지만

 

여기서 조금만 더 변형을 해서 쓸모있게 만든다. 

 

 

 

이므로 (x + y)(w + z), xw, yz 이렇게 세가지의 곱셈만 수행한다면 

이 식을 만족시킬 수 있고

 

다음과 같이 표현할  수 있다. 

Large_integer prod(large_interger u, large_integer v){
large_integer x, y, w, z, r, p, q;
int n, m;

n = max(number of digits in u, number of digits in v);
if(u == o || v == o) return o;
else if(n <= threshold) return u x v  //일반적인 방법을 이용
else{

m = n/2; 
x = u divide 10^m;
y = u rem 10^m;
w = v divide 10^m;
z = v rem 10^m;
r = prod(x + y, w + z);
p = prod(x, w);
q = prod(y, z);

return p x 10^2m + (r - p - q) x 10^m + q;

}
}

 

 

prod(x+y, w + z)의 단위 연산은 

위와 같으므로 n/2 <= input size <= n/2 + 1이 될수 있다.

 

따라서

이고, 도사정리에 의하면

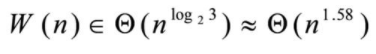
이므로 일반적인 큰 수의 곱셈보다 좋다고 할 수 있다.