알고리즘: 되추적(Backtracking) 공부하기! (N-Queens problem을 풀어보자)

되추적은 임의의 집합에서 주어진 기준대로 원소의 순서를 선택하는 문제를 푸는데 사용한다.

 

전형적인 사례로 체스의 n-Queens Problem이 있다.

 

 

 

 

이 문제의 목표는 n x n  크기의 서양 장기판에 서로 잡아먹히지 않도록 n개의 여왕말을 위치시키는 것이다.

 

즉, 어떤 여왕말끼리도 같은 행이나 열, 대각선상에 위치할 수 없다.

 

이 문제에서 순서는 여왕말을 둘 n개의 각각 다른 위치이고, 집합은 서양 장기판에서 말을

둘 수 있는 n제곱개의 위치들이 되고, 기준은 어떤 여왕말도 서로 잡아 먹히지 말아야 한다는 것이다. 

 

 

 

 

되추적은 트리의 변형된 깊이우선탐색(DFS)이다.

 

DFS에 대해 간단히 설명하면 부모의 노드에서 내려갈 수 있는 자식노드까지 내려가고 

 

그 이후의 자식 노드가 없다면 다시 부모노드로 돌아가면서 탐색하는 방식이다.

 

 

DFS로 탐색한 경우

 

 

 

 

 

그렇다면 n = 4인 4-Queens problem을 풀어보면서 DFS와 어떻게 다른지 확인해보자 

 

 

<4-Queens Problem 풀어보기>

 

먼저 이 문제를 brute force로 풀어보자

 

각 Queen들은 4개의 열 중에 한 곳에 놓을 수 있기 때문에 해답후보는 4 x 4 x 4 x 4 =256개이다.

 

 

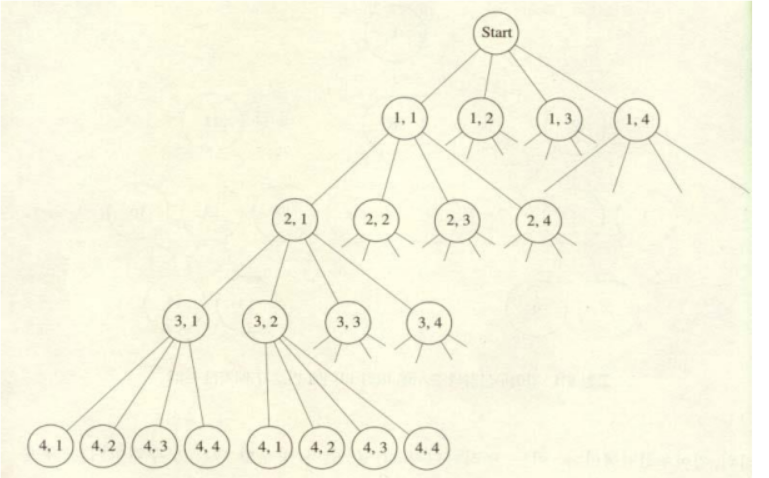
4-Queens 문제의 상태공간트리

 

brute force를 이용하여 해답후보들을 탐색해봤을 때 가능성이 전혀 없는 

 

자식노드들도 모두 검색해야하므로 비효율적이다. 

 

내려가봐야 해답이 없는 노드를 만나는 순간, 그 마디의 검색을 중단하고 그 마디의 부모노드로

돌아가서 다른 자식노드 검색을 계속하는 과정을 되추적이라 한다.

 

(되추적은 변형된 깊이우선탐색으로 깊이 우선탐색의 경우 promising하지 않은

노드 또한 검색한다)

 

여기서 해답이 될 가능성이 있는 노드를  유망하다(Promising)고 한다. 

 

정리하면 되추적은 상태공간트리를 깊이우선탐색하여 각 노드가 유망한지

검사하고, 만약 유망하지 않으면 그 마디의 부모노드로 되추적한다. 

 

이러한 절차를 가지친다(Prunning)이라고 하고 유망한 마디만으로 구성된

부분트리를 가지친 상태공간트리(Pruned state space tree)라 한다.  

 

 

 

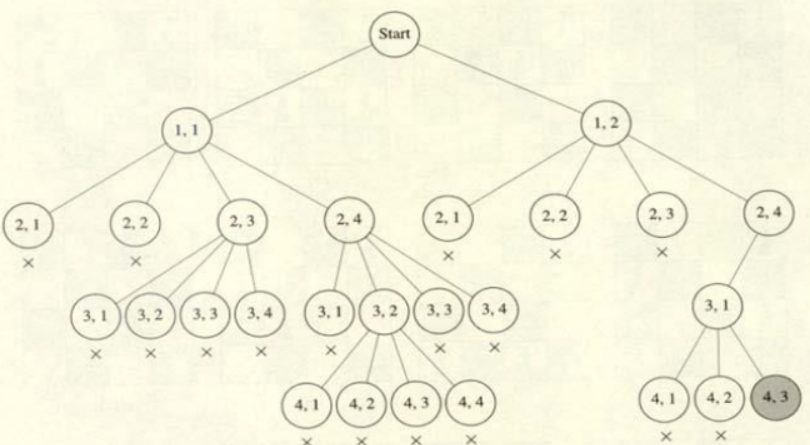
pruned state space tree

 

일반적인 dfs를 사용했을 때는 155개의 노드를 검색하는 반면

 

promising한 노드만을 탐색했을 때는 27개의 노드만을 검색하였다. 

 

 

 

DFS와 prunning을 이용하여 다음과 같은 수도코드를 만들 수 있다. 

 

void checknode(node v)
{
node v;

if(promising(v))  // 노드 v가 유망한가? 
	if(there is a solution at v) 
    	write the solution;
    else
    	for(each child u of v)  // 모든 노드에 대해서 깊이 우선 탐색
        	checknode(u);


}

 

 

 

 

 

그렇다면 여기서 promising함수는 어떻게 구성할까?

 

col(i)를 i째 행에서 여왕말이 놓여있는 열이라고 한다면 k번째 행에 있는 여왕말이

 

같은 열에 있는지 검사하기 위해서는 다음 등식이 성립하는지 검사해야한다. 

 

col(i) = col(k)

 

 

대각선은 다음과 같은 방식으로 검사한다. 

 

col(i) - col(k) = i - k 또는 col(k) - col(i) = k - i 이므로 

 

이를 이용해서 다음과 같이 코드로 나타낼 수 있다. 

 

 

void queens(index i){

	index j;
	if(promising(i))
    	if(i == n) cout << col[1] through col[n];
        else
        	for(j=1; j<=n; j++){
            col[i+1] = j;
            queens(i+1);
            }

}

 

bool promising(index i){
	index k;
    bool switch;
    
    k = 1;
    switch =TRUE;
    while(k<i && switch){
    	if(col[i] == col[k] || abs(col[i] - col[k]) == abs(i-k))
        	switch = FALSE;
        k++;
       
    }
	return switch;
}

 

 

 

위의 두 알고리즘을 고려하여 해답들을 확인해보면 모든 문제의 해답들을 만들어버린다. (우리의 의도와는 다른)

 

이론적으로 이 알고리즘을 분석하기는 어렵기 때문에 검사하는 마디의 수를 여왕말의 개수인

n의 함수로 나타내야 한다.

 

이를 일반화하면 

 

이지만 사실 이 분석은 별 가치가 없다. 

 

왜냐하면 되추적함으로써 점검하는 노드의 수를 얼마나 줄였는지 전혀 알 수 없기 때문이다. 

 

 

 

그래서 이번에는 유망한 노드만을 세어서 구해본다.

 

같은 열에 위치할 수 없다는 사실을 이용하여 다음과 같이 구한다. 

 

 

하지만 이 또한 대각선을 고려하는 경우를 고려할 수 없으므로 알고리즘의 복잡도를 정확히 말해주지 않는다. 

 

(즉, 이 모든 방법에는 의미가 없다)

 

 

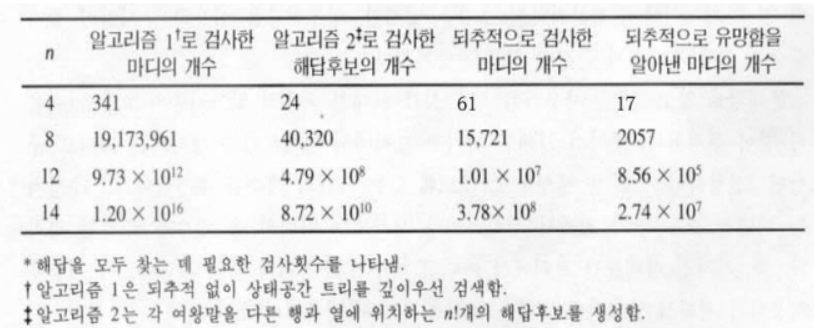
알고리즘 수행시간 비교

 

 

 

어떤 되추적 알고리즘이라도 유망함수를 실행하는데 걸리는 시간이 중요한 고려사항이다.

 

알고리즘의 목표는 검사 노드의 개수를 줄이는데만 있는게 아니기 때문에 전체적인 효율성을 고려해야한다.

 

그래서 다음 포스팅에서는 되추적 알고리즘의 효율성을 추정하기 위해 사용되는

몬테칼로 알고리즘에 대해서 알아보겠다. 

 

 

 

출처 : Foundations of Algorithms, Using C++ Pseudocode