알고리즘: 스케줄짜기(Scheduling)공부하기! (시스템 내부시간 최소화, 마감시간이 있는 스케줄짜기)

 

어떤 미용사에게 여러가지를 서비스를 받으려고 기다리는 손님이 있다고 하자.

 

서비스에 걸리는 시간은 모두 다르고 미용사는 얼마나 걸릴지 알고 있다.

 

손님들이 기다리는 시간을 최소가 되도록 손님을 서비스하는 것을 스케줄 짜기(sheduling)이라 하며 기다리고

머리하는데 걸리는 시간을 시스템 내부시간(time in the system)이라 한다. 

 

그리고 마감시간이 정해진 경우(scheduling with deadlines)가 있는데 각 작업을 끝내는데 같은 시간이 걸리지만

각 작업과 관련된 보상을 최대로 얻기 위해서 마감시간을 고려해야하는 경우다. 

 

이렇게 스케줄짜기는 시스템 내부시간(time in the system)과 마감시간이 있는 스케줄짜기(scheduling with deadlines)로 나뉘며 이 둘에 대해서 알아본다. 

 

 

 

 

 

1. 시스템 내부시간의 최소화

 

 

세가지 서비스가 있다고 했을 때 걸리는 시간은 다음과 같다고 하자

 

 

 

이 때 기다려야 하는 경우의 수는 총 3!으로 6가지이다. 

 

 

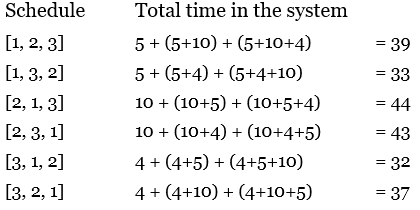
직관적으로 봤을 때, 짧은 작업 시간순으로 작업수행을 했을 때 최적의 작업시간을 갖는다..

 

이렇게 알고리즘은 정렬 후, 값을 더하므로 실제 시간복잡도는 다음과 같다. 

 

 

 

 

 

더 나아가서 이 알고리즘을 복수 작업자 스케줄짜기 문제(mulitple-server scheduling problem)으로

일반화하기 쉽다.

 

작업자가 m명 있다고 가정했을때 작업자의 순서는 무작위다. 

 

작업시간별로 작업을 비내림차순으로 정렬한다.

 

첫째 작업자는 첫째 작업을 하고, 둘째 작업자는 둘째 작업을 하고, ... m번째 작업자는 m번째 작업을 한다.

 

m번째 작업자가 작업을 끝낸 후, 첫번째 작업자는 m+1번째 작업을 한다. 

 

 

 

 

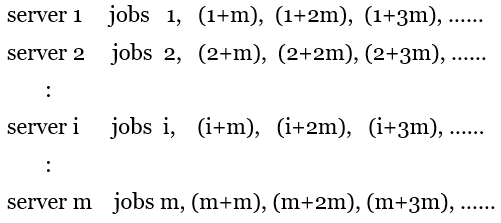
그리고 결과적으로는 전체를 비내림차순으로 정렬하여 다음 순서로 처리하게 된다. 

 

 

 

 

 

 

2. 마감있는 스케줄짜기(Scheduling with deadlines)

 

마감시간이 있는 스케쥴 짜기에서는 모든 작업들이 끝나는데 걸리는 시간이 같고 마감시간과 보상이 할당되어 있다.

 

작업을 마감시간 전이나 마감시간에 마친다면 보상을 받으며

 

목표는 마감시간안에 작업을 끝내서 최대의 보상을 얻는 것이다. 

 

 

 

다음과 같은 문제를 통해서 살펴보자 

 

 

 

2번 작업과 4번 작업은 마감시간이 1이므로 두번째 열에 오지 못한다.

 

따라서 6가지의 경우의 수를 갖고 

 

이렇게 마감시간안에 작업을 끝내서 최대의 보상을 얻는 경우는 [4, 1]의 경우다.

 

 

 

 

마감시간안에 스케줄링하는 알고리즘을 살펴보기 전에 몇가지를 정의해보자

 

적절한 순서(feasible sequence): 작업순서상의 모든 작업들을 마감시간안에 끝내는 경우

적절한 집합(feasible set): 작업의 집합에서 적당한 순서가 존재하면 그 집합은 적절한 집합이라고 한다. 

최적순서(optimal sequence): 총 보상을 최대로 하는 적절한 순서

최적 집합(optimal set): 순서에 속한 작업의 집합 

 

 

 

 

위의 개념들을 알아보기 위해 deadline이 3까지 있고, 7개의 작업이 있는 경우에 대해 살펴보자 

 

우선 profit이 큰 순서로 내림차순 정렬을 한다.

 

 

 

1. S를 공집합으로 설정한다.

2. 순서 [1]이 feasible하므로 S를 {1}로 설정한다.

3. 순서 [2, 1]이 feasible하므로 S를 {1, 2}로 설정한다.

4. {1, 2, 3}에 대해서는 feasible한 순서가 존재하지 않으므로 3은 기각!

5. 순서 [2, 1, 4]이 feasible하므로 S를 {1, 2, 4}로 설정한다.

6. 이후부터는 적절한 순서가 존재하지 않으므로 모두 기각!

 

 

결론적으로 최종 feasible set이 {1, 2, 4}인 경우 최대의 보상을 얻을 수 있다. 

 

 

 

 

이제부터는 알고리즘이 어떻게 생겼는지 살펴본다.

 

deadline이 profit순으로 내림차순 정렬되어 있다고 할때 알고리즘은 다음과 같다. 

 

void schedule(int n, const in deadline[], sequece_of_integer& J){

index i;
sequence_of_integer K;  // feasible sequence 
J = [1];  // feasible set

for(i=2; i<= n; i++){  
K = J에다가 deadline[i]의 i값을 추가한다;
if(K가 적절하다) // 적절하다면 feasible set을 새롭게 갱신
J = K
}
}

 

 

위의 알고리즘을 적용해봤을 때 

 

 

1. J는 [1]이 된다.

2. K는 [2, 1]이 되고 feasible하므로 J를 [2, 1]로 갱신한다.

3. K는 [2, 3, 1]이 되고 feasible하지 않으므로 기각!

4. K는 [2, 1, 4]이 되고 feasible하므로 J를 [2, 1, 4]로 갱신한다.

5. 이후부터는 모두 feasible하지 않으므로 모두 기각! 

 

 

 

 

시간복잡도는 각각의 iteration에 대해서 i번 반복되므로